Vous cherchez un moyen d’augmenter la satisfaction de la clientèle? Avez-vous pensé que le temps takt peut vous y aider?
Rappelons que le terme « takt » provient du latin tactus et de l’allemand takt. Il fait référence à la cadence à laquelle quelque chose se déroule. Le temps takt peut donc se définir comme le temps entre la réalisation consécutive de deux actions similaires.
Dans un contexte Lean, le temps takt est la durée à l’intérieur de laquelle un produit ou un service doit être réalisé pour respecter la demande du client.
La première utilisation connue du terme « takt » remonte aux années 1930 chez le manufacturier aéronautique allemand des bombardiers Junkers Ju 87 utilisés pendant la Seconde Guerre mondiale.
Lorsque la demande du client est connue à l’avance, comme c’est souvent le cas dans un environnement manufacturier, il n’est pas difficile de comprendre et d’appliquer le temps takt. Mais qu’en est-il lorsque le processus d’affaires s’avère plus complexe, par exemple lorsque les clients se présentent en ordre dispersé?
C’est ce dont le Dr Steve Kramer a discuté dans cette présentation faisant partie du profil « Advanced Content Masters Series » de la conférence de l’ASQ. Le Dr Kramer est professeur associé en sciences de la décision (Nova Southeastern University) et maître Ceinture noire (ASQ).
Voyons ce que nous dit le Dr Kramer.
Un rappel pour commencer : afin de considérer la variabilité de la demande à l’intérieur d’un temps takt donné, il faut se baser sur le principe selon lequel le temps entre deux arrivées aléatoires de clients suit typiquement une distribution de Poisson.
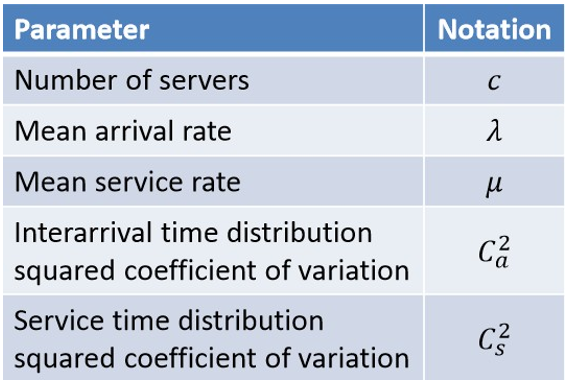
Voici maintenant les paramètres en intrants qui influenceront le niveau de congestion dans le service à la clientèle :
Les tableaux qui suivent proviennent du fichier PowerPoint du Dr Kramer et sont donc en anglais.
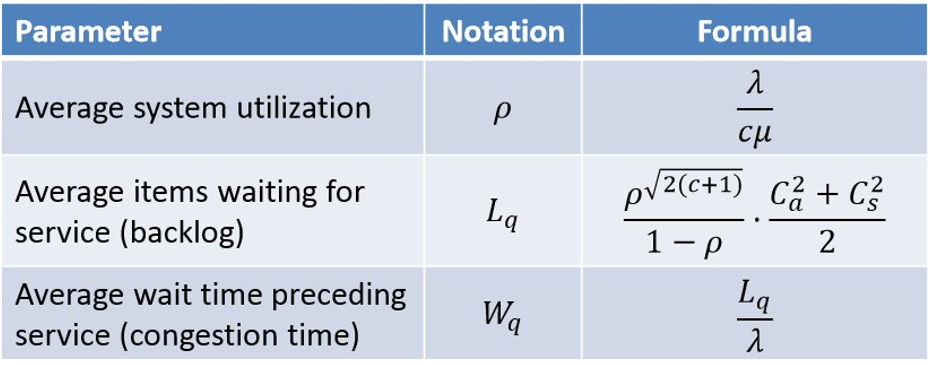
En utilisant comme intrants les paramètres ci-dessus, on peut déterminer les extrants suivants :
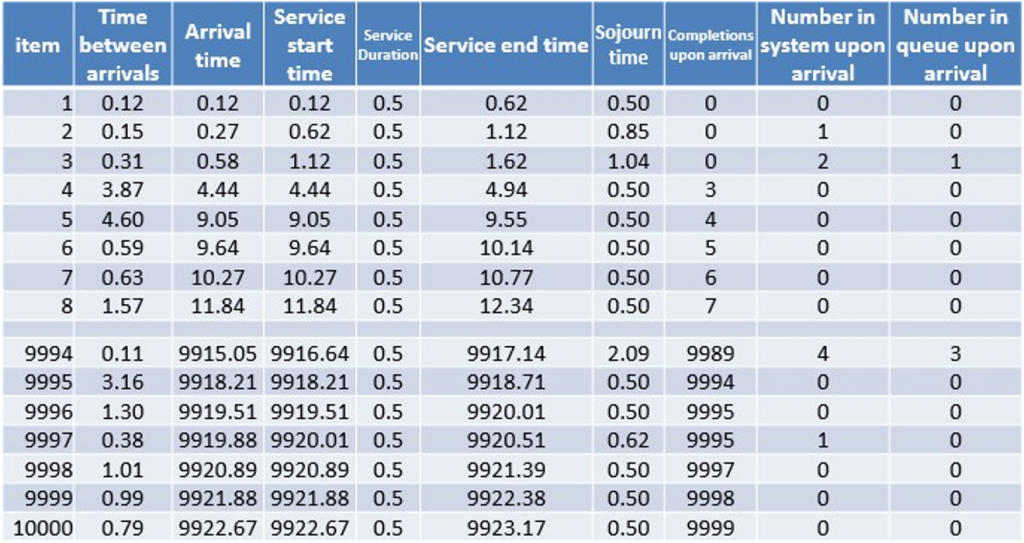
Supposons que nous avons 10 000 intervalles entre deux arrivées selon la distribution de Poisson. Pour les fins de cet exercice, on suppose qu’il n’y a aucune variation dans le temps de service (toujours égal à 0,5), ce qui génère un carré du coefficient de variation du temps de service (Cs2) égal à zéro.
Dans le tableau ci-haut :
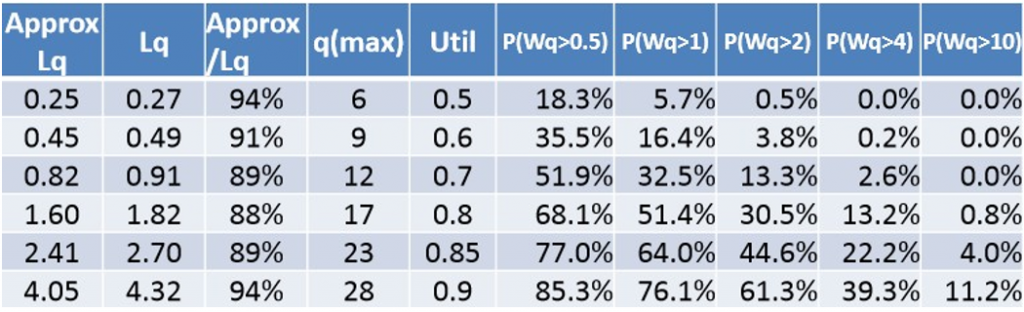
En simulant le traitement de ces 10 000 arrivées selon divers taux d’utilisation moyens du processus (ρ ou Util dans le tableau ci-après), on obtient un tableau de probabilités où le temps de congestion dépasse certaines durées spécifiques (colonne P(Wq>t)).
Par exemple, considérant un processus utilisé à 70 %, 13,3 % des clients ont passé plus de deux unités de temps (minutes, secondes, etc.) dans le processus.
Pour minimiser la congestion dans le service à la clientèle lorsque la demande est aléatoire, la clé est d’éviter la tentation de « surutiliser » le processus. Il s’agit plutôt d’adapter le nombre de serveurs ou d’agents disponibles (c) et le taux de service moyen (µ) à un niveau tel que le taux d’utilisation moyen du processus (ρ) n’excède pas un niveau générant trop de risque de congestion pour la clientèle.
La leçon est donc claire : pour gérer notre capacité de répondre à la demande, il faut se baser sur notre niveau de tolérance au risque de congestion.
Remarquons par ailleurs que les clients qui se présentent avant la disponibilité d’un serveur constituent une forme de gaspillage : le serveur ne peut en effet exécuter de travail préparatoire dans le but de diminuer son temps de service. Un client qui arrive trop tôt doit donc d’une certaine façon être « stocké », avec tout ce que cela comporte de risques assimilables à ceux de la gestion des stocks ! Et cette période à non-valeur ajoutée s’ajoute au temps de service du client.
En contrepartie, les clients qui se présentent après la disponibilité d’un serveur génèrent un gaspillage de serveurs « en attente », mais minimisent le temps de service expérimenté par le client.
Or, il est mathématiquement possible de trouver le meilleur compromis entre les clients hâtifs et les clients retardataires.
Un autre point digne de mention est que la congestion est en principe observable seulement à l’entrée de la première étape du processus. Il est possible de minimiser cette congestion à l’aide d’un régulateur (p.ex. kanban) qui s’assure de minimiser la variation des arrivées. La congestion subséquente peut être par la suite évitée, même en présence d’un haut taux d’utilisation du processus, si la variation du temps de service est minimisée.
Bref, pour bien appliquer la notion de temps takt et ainsi minimiser la congestion dans notre processus de service à la clientèle, le Dr Kramer a mathématiquement démontré l’importance de deux variations :
Lorsque ces deux objectifs sont atteints, il est plus facile de concevoir un processus de service à la clientèle qui augmentera le niveau de satisfaction des clients en termes de temps de réponse.
Vous voudriez avoir à votre disposition de puissants outils Lean ou statistiques comme celui décrit dans cet article pour vous attaquer à des problèmes dans votre organisation? Inscrivez-vous à notre formation Ceinture noire Lean Six sigma!
Il semble que vous n'ayez pas encore fait de choix.