Stratification, histogramme et diagramme de dispersion

Faire parler visuellement les informations

Illustrer visuellement une situation est un art. En effet, plusieurs conclusions peuvent être tirées lors de l’analyse de graphiques ou de diagrammes en résolution de problèmes. Ces derniers sont une aide précieuse dans les phases de description et de compréhension d’une situation ou de l’analyse des causes potentielles d’un problème.

Résultats

• Représentation visuelle claire facilitant l’analyse des données en résolution de problèmes.
• Image simple permettant de constater des tendances sur des indicateurs donnés.
• Illustration de la distribution d’une variable (histogramme).
• Comparaison de la variation d’une situation avec la courbe normale ou avec des variations provenant d’échantillons différents (histogramme).
• Établissement de l’existence ou non d’une relation entre deux phénomènes (dispersion).
• Vérification de ce qui arrive à un phénomène quand un autre phénomène varie (dispersion).

Conditions de succès

• Toujours s’assurer de bien sélectionner les situations à comparer et la période étudiée.
• Vérifier les échelles (base = zéro ou valeur minimale) ainsi que leur identification (titre de l’axe et unités).
• Inscrire un titre de graphique représentatif et, selon le cas, le lieu, la date, l’origine, l’auteur, etc.
• Bien faire ressortir les phénomènes sans créer de grossissement excessif des écarts (graphique à colonnes et graphique linéaire).
• Utiliser la catégorie « divers » uniquement pour représenter moins de 25 % de l’ensemble (graphique circulaire).
• Éviter les conclusions hâtives.
• Analyser un seul phénomène à la fois.
• Disposer d’un nombre suffisant de données.

Méthode

Stratification

La stratification consiste à diviser des informations ou une population en strates. Les graphiques permettent de représenter les strates sous forme visuelle. Il existe trois grandes catégories de représentations :

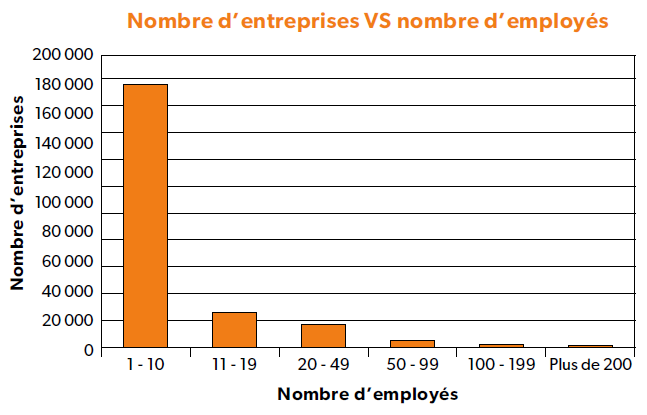
1. Le graphique à bandes ou à colonnes est un outil de comparaison qui présente les situations caractérisant différents secteurs, groupes, individus, etc.
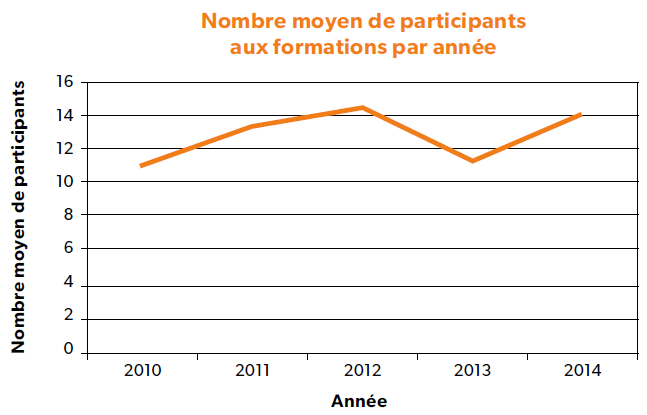
2. Le graphique linéaire illustre l’évolution d’une ou de plusieurs situations dans le temps.
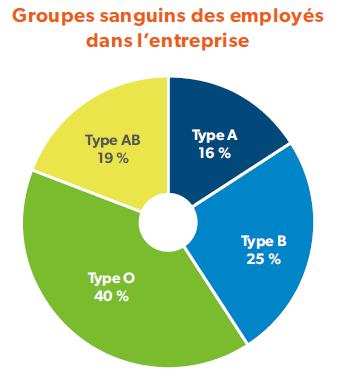
3. Le graphique circulaire, que l’on compare souvent à une tarte divisée en pointes, représente les différentes parties d’un tout et met en évidence l’importance relative de chacune de ces parties les unes par rapport aux autres.

1. Graphiques à bandes ou à colonnes

Représenter graphiquement des données quantitatives pour être en mesure de voir l’importance relative de chacune des composantes d’un élément. En utilisant deux bandes ou plus, on peut également comparer chacun des éléments et chacune de leurs composantes afin d’apprécier leur différence proportionnelle.

2. Graphique linéaire

Représenter graphiquement l’évolution d’un ou de plusieurs indicateurs. Surtout utilisé pour apprécier le changement relatif entre les intervalles de mesure, il permet d’analyser les tendances en fonction du temps.

3. Graphique circulaire

Son but est de représenter des données quantitatives et mettre en évidence l’importance relative de chacun des éléments. La représentation circulaire permet de visualiser facilement les proportions relatives sous forme de pourcentage.

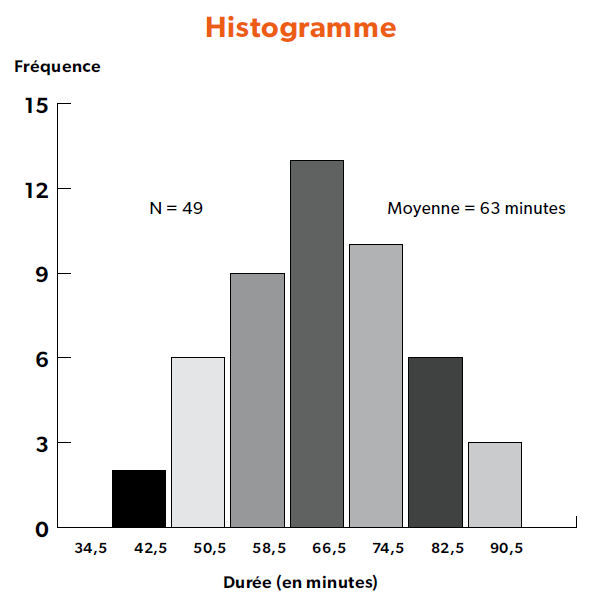
Histogramme

L’histogramme est un type de graphique à colonnes qui représente la distribution de données quantitatives relatives à un phénomène.

Il permet de représenter une série de données pour en visualiser le type de distribution, la tendance centrale et leur dispersion. L’outil prend habituellement la forme d’un graphique à barres représentant les fréquences d’une série de données réparties en plusieurs classes ou cellules.

1. Recueillir les données relatives au phénomène à illustrer (ex. 49 données).
2. Établir une table de fréquence à partir de l’ensemble des données :
   – classer les données en ordre croissant ou décroissant;
   – déterminer les valeurs minimale et maximale (ex. 35 min. et 90 min.);
   – calculer l’étendue : valeur maximale moins valeur minimale (90 – 35 = 55 min.);
   – déterminer le nombre de classes : racine carrée du nombre de données (ex. racine carrée de 49 = 7);
   – calculer l’amplitude des classes : étendue des données divisée par nombre de classes (ex. 55 ÷ 7 = 8);
   – établir la limite inférieure de la première classe : valeur minimale moins [unité de mesure divisée par 2] (ex. 35 – [1 min. ÷ 2] = 34,5);
   – élaborer un tableau où les limites de classes seront inscrites dans la première colonne, les observations ou phénomènes dans la deuxième et le total de celles-ci (les fréquences) dans la troisième.
3. Réaliser l’histogramme à partir de l’ensemble des données.

DIAGRAMME DE DISPERSION

Le diagramme de dispersion, aussi appelé de corrélation, illustre la relation entre deux phénomènes à partir de deux groupes de données.

1. Recueillir les données relatives aux phénomènes à mettre en relation : chaque cas doit être caractérisé par une paire de données, par exemple le poids et la taille de chaque individu, pour être en mesure d’effectuer une corrélation.
2. Placer les données sur le tableau (une catégorie par axe).
3. Analyser le graphique obtenu.

Références

• The 7 Basic Quality Tools for Process Improvement. ASQ. Consulté le 2019-06-12.
• Seven Basic Tools of Quality. What Is Six Sigma. Consulté le 2019-06-12.